The UPSCALE project (Upscaling Product development Simulation Capabilities exploiting Artificial intelligence for electrified vehicles) is celebrating its second year of implementing Artificial Intelligence (AI) in the process of developing electric vehicles, under the framework of the European Union’s R&D incentive programme, Horizon 2020 (grant agreement no. 824306).
Algorithmica Technologies GmbH (Germany), Applus+ IDIADA (Spain), Centro Ricerche Fiat SCPA (Italy), École Nationale Supérieure d’arts et métiers (France), Engys Ltd (UK), ESI Group (France), FI Group (Spain), Kompetenzzentrum- Das Virtuelle Fahrzeug Forschungsgesellschaft mbH (Austria), Volkswagen AG (Germany), Volvo Personvagnar AB (Sweden) y Vrije Universiteit Brussel (Belgium).
Here some news:
Aerodynamics
CFD process acceleration
Machine learning algorithm require huge amounts of data to train to usable levels of accuracy. In the context of vehicle aerodynamics, the method of choice for generating base-truths is CFD. CFD is however computationally expensive, especially for the levels of accuracy typically required for automotive aerodynamics. The CFD process consists off several different steps, all of which can be enhanced to improve the performance of the prediction.
Grid generation
High fidelity CFD calculations require large meshes with complex shapes and topology. With the accelerated solers developed during the program, the mesh generation becomes the most expensive part of the process. To alleviate this bottleneck, we employ state-of-the-art OpenVDB level-set libraries to accelerate surface handling and volume mesh generation. OpenVDB exploits a very fast and efficient data structure and is the de facto standard for volumetric data handling in the visual effect industry. Preliminary results suggest a performance gain of up to 10 times.
Setup
Choosing realistic initial conditions for aerodynamic flow fields can lead to significant improvement in solution times. A reasonable option is to map results from a similar case to provide a good starting point. A new mapping algorithm was introduced to accelerate performance by more than an order of magnitude. Machine learning classification algorithm is used to select the source case with the closest feature vector to the target case. This in combination with wall distance mediated smart mapping, provides initial fields with exceptionally high correspondence to the eventual results, resulting in average solution time reduction in large DoEs of 33%. The enhanced search used in the mapping is also employed to accelerate spatial data sampling.
Solver
Block coupled solution algorithms are more complex and memory-intensive than traditional solution methods, but offer the potential for much higher performance. Previous experience in this context was leveraged to develop a new block matrix solution system that can reach a converged state 2-3x faster than heavily optimised traditional segregated methods. Overall, the new toolchain will execute a large design of experiments roughly 3 times faster than was possible before, saving hundreds of thousands of core hours and months of execution time during the project alone.
PIML Turbulence models
The Physics Informed Machine Learning (PIML) based Turbulence modeling aims at improving the accuracy of low fidelity (RANS) CFD simulation methods by training ML algorithms on the available high fidelity (DNS) data sets. This is achieved by quantifying the relationship between Reynolds stresses (R) and several mean flow fields via training the non-linear regression based PIML model. Ultimately this ML toolbox is used to recompute turbulent R and resulting flow statistics in RANS simulations.
A framework that gathers up to 10 mean flow parameters and the R tensor from RANS and DNS simulations has been implemented in order to train the PIML model. Inherently, it is capable to use the training data independent of chosen cartesian frame, geometry, CFD flow domain sizes etc. if each grid cell used in the training phase has exactly the same ML input and output parameter dimensions.
The initial results from PIML framework shows good agreement of the predicted turbulent stresses as compared to the DNS results as illustrated in the below figures with contour lines at exactly same magnitudes of R. The framework is trained using the 2D DNS simulations of backward facing step cases at two different flow Reynolds numbers, which then is used to predict the R tensor over a backward facing step case with flow Reynolds number difference of 8.3% as compared to the training database.



(d) Error between DNS and PIML
3D Vehicle parametrization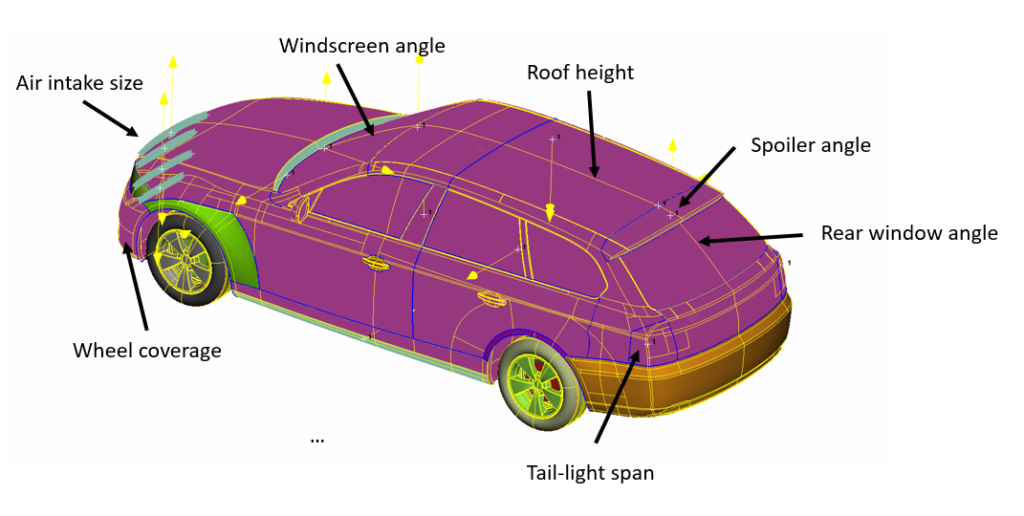
Geometry parametrization of the external shape of the vehicle is a key point in the aerodynamic optimization process: this stage, required for the generation of different shapes that will feed machine learning and optimization algorithms, needs to be as fast and robust as possible, ensuring always good quality geometry to be analyzed by CFD simulations. To overcome these possible bottlenecks, an automated parametrization tool has been developed and tested on a 3D-DrivAer model. The utility is able to generate up to twenty “standard” morphing parameters, such as spoiler inclination, windscreen angle, rear-end taper ratio, …
The tool has been used by UPSCALE partners to parametrize three different kind of vehicles: a Volvo full electric XC40 SUV, an FCA 500e full electric city car and a Volkswagen hybrid Jetta limousine. These models will be used as test cases to validate the aerodynamic optimization process driven by machine learning techniques on actual production vehicles.
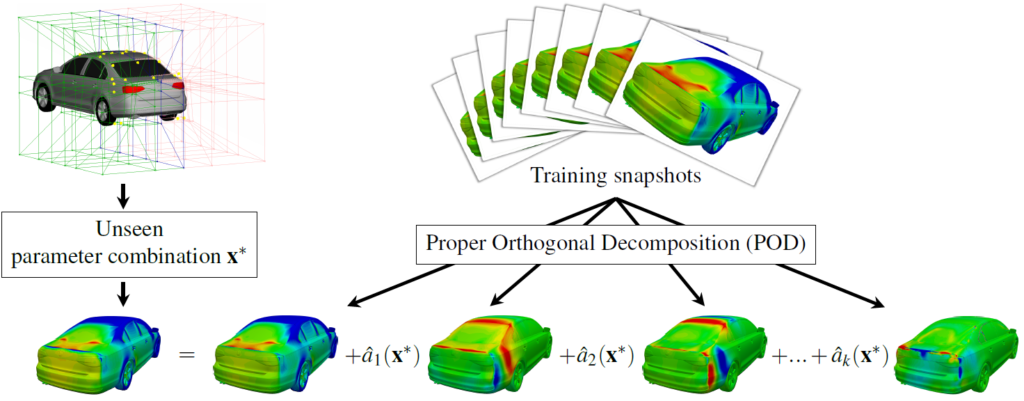
H3 POD-based aerodynamics ROM
Illustration of the POD+I method: Shown are the pressure POD modes. Their linear combination with suitably interpolated POD base mode coefficients âj serves as the pressure prediction for an unseen geometry represented by the parameter set x^* (reproduced from [1]).As a baseline reference for the benchmarking of the Neural Network-based prediction methods to be developed within UPSCALE, we decided to apply the well-known deterministic “POD+I” paradigm (Proper Orthogonal Decomposition + Interpolation, to the 2D-DrivAer test case provided by the UPSCALE partner CRF. Since the interpolation part of POD+I suffers from the “curse of dimensionality”, it was an open question, if this method delivers results of satisfactory accuracy also for this 14-dimensional test case. But preliminary results indicate that the errors in the predictions of fields and coefficients are comparable to those encountered, where a 6-dimensional car test case was treated with the same approach.
Aerodynamics ROM based on universal parametrization
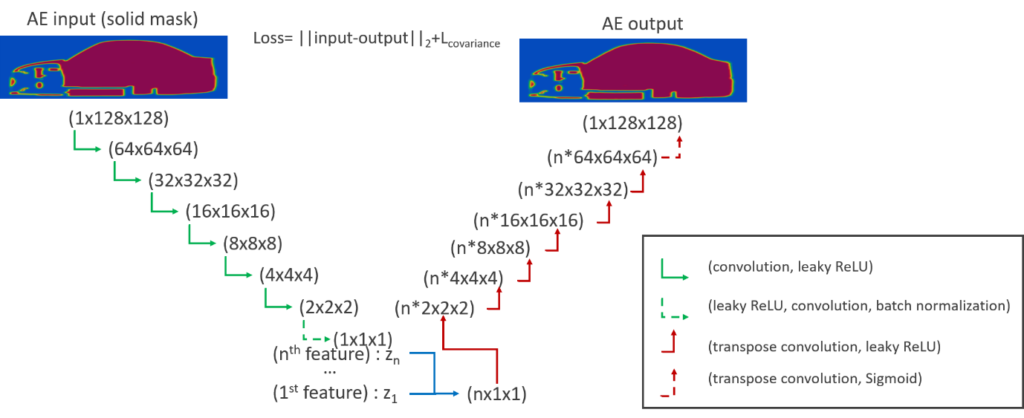
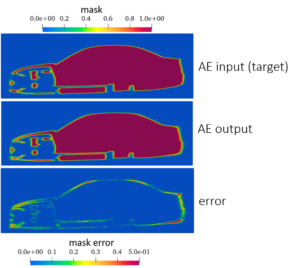 A state-of-the-art autoencoder (AE) is employed for automatic parametrization of the vehicle geometry. The autoencoders are considered to be a self-supervised form of ML and they typically consist of the encoder, where the input information is compressed into a lower-dimensional space (latent), and the decoder, where the output is reconstructed from the latent space. The developed AE shares the attributes of Principal Component Analysis, i.e. the parameters are hierarchical and independent while maintaining non-linearity at the same time. The decreasing importance of the parameters is achieved by performing iterative training and thus, the latent space is incrementally increased by 1 feature. To achieve independence of the latent space parameters, a covariance term in the loss function is introduced. The input is the same as the output and it is the sampled geometry mask, either in a scalar or in a level-set field. Overall, the AE reconstructs the input with an error of 3-4%. As an alternative to the classification algorithm for predicting the drag coefficient, the AE latent space can be used in a regressor method. The error in the latter has been documented to be 5-6%.
A state-of-the-art autoencoder (AE) is employed for automatic parametrization of the vehicle geometry. The autoencoders are considered to be a self-supervised form of ML and they typically consist of the encoder, where the input information is compressed into a lower-dimensional space (latent), and the decoder, where the output is reconstructed from the latent space. The developed AE shares the attributes of Principal Component Analysis, i.e. the parameters are hierarchical and independent while maintaining non-linearity at the same time. The decreasing importance of the parameters is achieved by performing iterative training and thus, the latent space is incrementally increased by 1 feature. To achieve independence of the latent space parameters, a covariance term in the loss function is introduced. The input is the same as the output and it is the sampled geometry mask, either in a scalar or in a level-set field. Overall, the AE reconstructs the input with an error of 3-4%. As an alternative to the classification algorithm for predicting the drag coefficient, the AE latent space can be used in a regressor method. The error in the latter has been documented to be 5-6%.
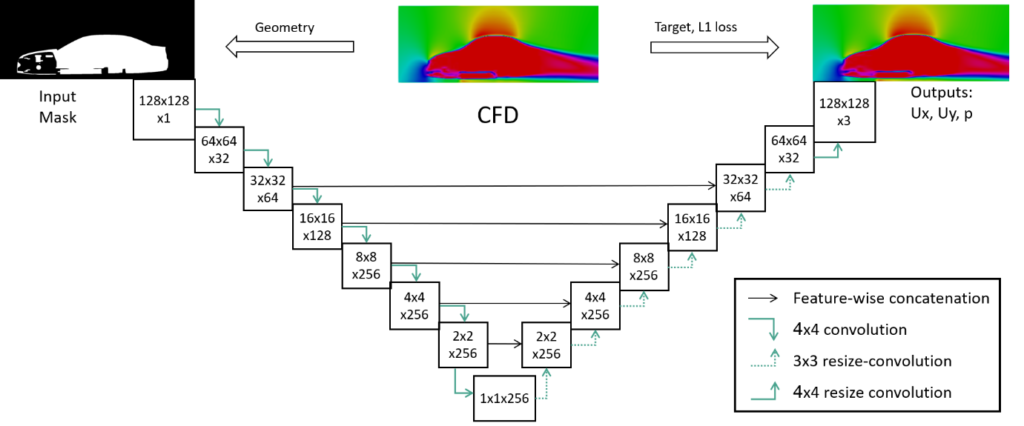
Neural networks for vehicle aerodynamic flow prediction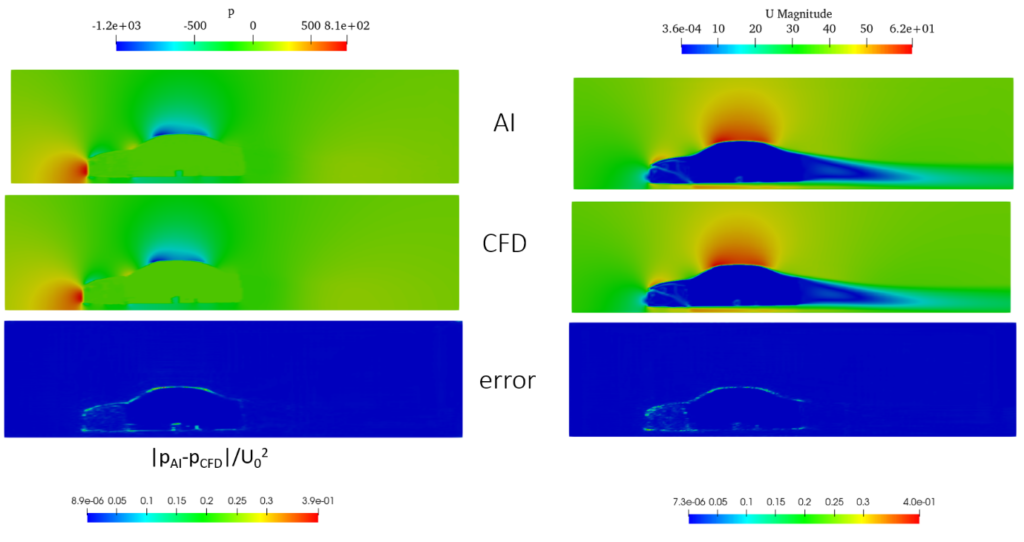
The pressure and the velocity flow fields around the vehicle, as well as the drag coefficient, are predicted by utilizing machine learning (ML) approaches. In order to train the artificial neural network (ANN), a database, which consists of several variations of the baseline geometry, is generated. CFD analysis is performed for each sample of the database and therefore, the volumetric flow fields and the drag coefficient are calculated, which will be later on used as targets for the corresponding ML algorithms. Regarding the volumetric flow fields prediction, a U-net architecture is used, whereas the drag coefficient is predicted by a classification algorithm. The input for both algorithms is the sampled geometry mask, either in a scalar or in a level-set field. The pressure-flow field prediction is 93%-97% accurate, the velocity vector field is above 99% accurate, whereas the drag coefficient is around 97% accurate.
Batery
Batery Cell Model
Basically, in modelling Li-Ion cells for crash applications, two different principle approaches and combinations thereof are in use. There is the so called macro-scale approach and there is the so called meso-scale approach.
Macro-scale
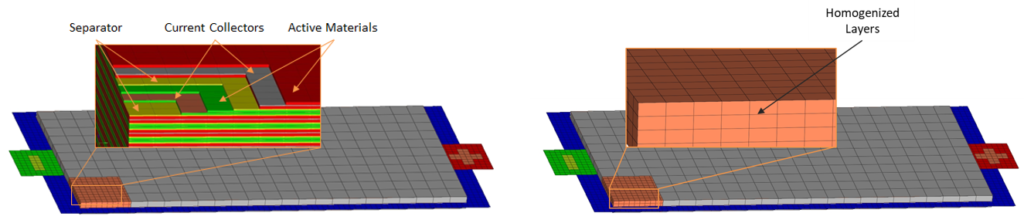
Macro-scale models combine the mechanical behaviour of all single layers of the active cell material to a fictitious homogenous material.
This leads to fewer elements and a higher time step. These models are therefore suitable for calculations in higher production levels such as battery module, battery pack and full vehicles. A short circuit detection can only be based on empirical criteria. The macro-scale approach will be used in the UPSCALE project with a validation based on results of the meso-scale model.
|
|
Macro-scale cell |
| Solid Elements | 6 608 with ~3mm |
| Shell Elements | 12 808 with ~2mm |
| Nodes | 21 256 |
| Initial Time Step | ~3.73E-04ms |
| Calculation time | <10min for 10ms (32 CPU) |
Meso-scale
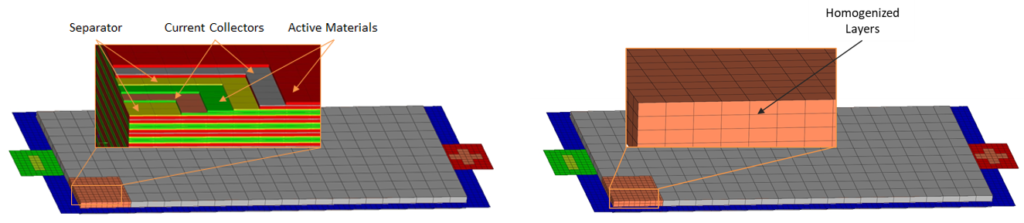
Every single layer of the active cell material is homogeneously modelled as a single component. By this method, an electrode is build-up out of the three layers of active material, current collector and active material. This leads to a highly detailed model which allows the assessment of the safety-critical separator layer. Depicting the actual physical structure of a cell though leads to a numerically expensive model with a high number of small elements with a consequently small calculation time step and very long calculation time. Due to these facts, meso-scale models are not suitable for the implementation of full vehicle crash simulation models. Advantages of these models are their potential accuracy and short circuit detection based on physical material parameters whereby the cell short circuit can be localized down the involved layers and characterized by the specific material combinations.
| Meso-scale cell | |
| Solid Elements | 4 455 034 |
| Shell Elements | 250 575 |
| Nodes | 8 779 883 |
| Initial Time Step | ~0.19E-04ms |
| Calculation time | <20h for 10ms (128 CPU) |
ROM for FEM simulation
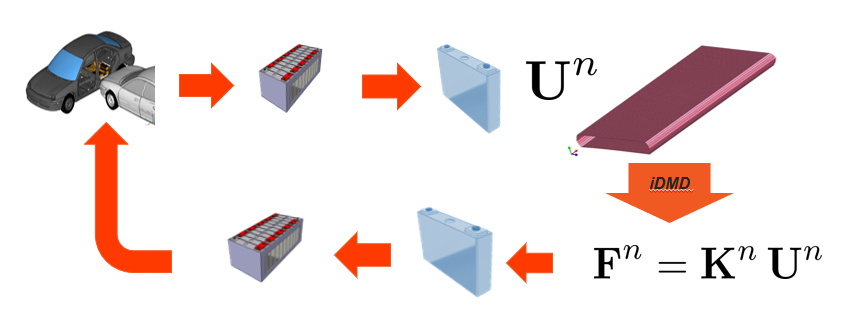 An EV battery pack includes modules and cell components and cannot be modeled as a detailed FEA model given the number of elements needed and time step requirements of explicit scheme in rapid dynamics. Thus, an equivalent ROM rigidity model is built as an alternative of the pure FEA homogenized model. The reduced-order model is built via a model learner based on Incremental Dynamic Mode Decomposition (iDMD) and Proper Orthogonal Decomposition (POD) where only the envelope (shell elements) of the cell is considered and to which an
An EV battery pack includes modules and cell components and cannot be modeled as a detailed FEA model given the number of elements needed and time step requirements of explicit scheme in rapid dynamics. Thus, an equivalent ROM rigidity model is built as an alternative of the pure FEA homogenized model. The reduced-order model is built via a model learner based on Incremental Dynamic Mode Decomposition (iDMD) and Proper Orthogonal Decomposition (POD) where only the envelope (shell elements) of the cell is considered and to which an
“equivalent rigidity” is computed at each time step to replace the jelly (solid elements) removed. This equivalent rigidity links the kinematics fields (displacements) to the reaction forces. An executable is delivered in D3.2 for the two stages: (i) training stage (ii) online stage. Due to the large number of unknowns that we are dealing with (~10k), a very large number of data would be needed to improve the model learner: from real loadings coming from car crash enriched by the parametric solution built via sparse PGD and elementary solicitations.
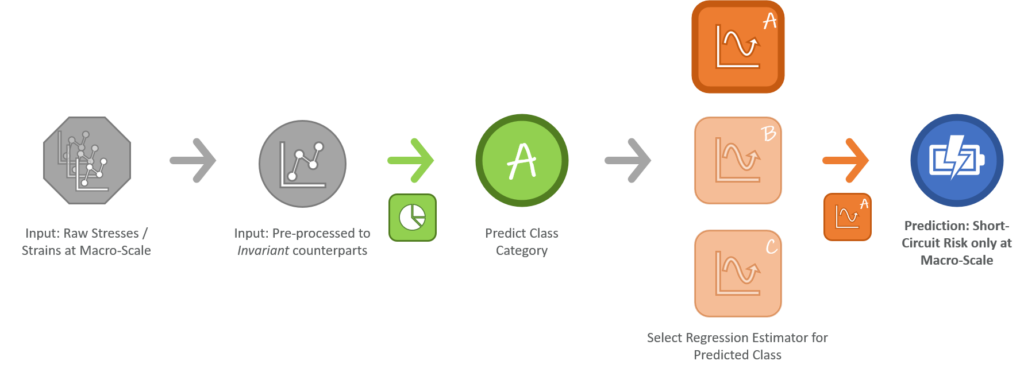
Battery ROM for short-cut prediction
FEA cell models have been generated within the UPSCALE project at meso and macro (homogenized) scales. From the macro-scale stresses and strains can be computed along with the battery cell. From the meso-scale, the battery short-circuit risk can be calculated. However, to get an accurate a battery short-circuit risk, the meso-scale computation is time and resources consuming and incompatible with full EV crash simulation.
Thus, a data-driven machine learning model is built based on the stresses and strains at the macro-scale and the battery short-circuit risk at the meso-scale for the training part. The online application of this data-driven model can predict the battery short-circuit risk based only on stresses and strain histories of the macro homogenized model. For training the data-driven model risk prediction, tens of unitary load cases are applied and measured on the cell at macro and meso scales. For better accuracy, different short-circuit risk-prediction models are trained independently for several classes of load cases. However, this method implies knowing the load case prior to predicting the short-circuit risk. This can be achieved by a first classification data-driven machine learning model that first predicts the load case. The combined approach enables a cell predicting the short circuit risk within 5% of the very detailed model with a computing cost compatible with full EV crash.